一、题目:
一根长度为n的绳子,剪成m段,m,n都大于1,且都为整数,每段长度记为k[0],k[1]…,k[m].求k[0]*k[1]…*k[m]可能的最大乘积
1.1解法:
两种不同的方法解决这个问题,先用常规的需要O(n²)时间和O(n)空间的动态规划,接着用只需要O(1)的时间和空间的贪心算法。
二、动态规划:
(1)是求最优解问题,如最大值,最小值;
(2)该问题能够分解成若干个子问题,并且子问题之间有重叠的更小子问题。
2.1通常按照如下4个步骤来设计一个动态规划算法:
(1)刻画一个最优解的结构特征;
(2)递归地定义最优解的值;
(3)计算最优解的值,通常采用自底向上的方法;
(4)利用计算出的信息构造一个最优解。
2.2用动态规划分析问题
首先定义函数f(n)为把长度为n的绳子剪成若干段后各段长度乘积的最大值。在剪第一刀的时候,我们有n-1中可能的选择,也就是剪出来的第一段绳子可能长度为1,2,…,n-1。因此f(n) = max(f(i) * f(n-i))。其中0<i<n。
2.3代码实现:
int maxProductAfterCutting_Solution(int length)
{
//绳子在3米以内,直接返回对应的值,不能用动态规划的公式做
if(length<2)
return 0;
if(length==2)
return 1;
if(length==3)
return 2;
//创建数组存储子问题最优解
int* products=new int[length+1];//?
//绳子大于3米,可以用动态规划的公式做,f(n)=f(i)*f(n-i)
//对于绳子长度为1,2,3米的,绳子的最大乘积就是长度本身
products[0]=0;
products[1]=1;
products[2]=2;
products[3]=3;
int max=0;
//从4米开始计算,直到计算到总长
for(int i=4;i<=length;++i)
{
max=0;
//对于长度为i的绳子,计算所有可能的切分,找到最大值
for(int j=1;j<=i/2;++j)
{
//切分组合
int product=products[j]*products[i-j];
if(max<product)
max=product;
products[i]=max;
}
}
max=products[length];
delete[] products;
return max;
}
三、贪心算法:
在每一步求解的步骤中,他要求每一步都是最优选择操作,并且通过一系列的最优选择,能够产生一个问题的(全局的)最优解
3.1 贪心算法满足的条件
1、可行的:即它必须满足问题的约束
2、局部最优:他是当前步骤中所有可行选择中最佳的局部选择
3、不可取消:即选择一旦选出,在算法的后面步骤就不可更改了
3.2 用贪心算法分析问题
如果我们按照如下的策略来剪绳子,则得到的各段绳子的长度的乘积将最大:当n≥5时,我们尽可能多的剪长度为3的绳子:当剩下的绳子长度为4时,把绳子剪成两段长度为2的绳子。
3.3代码实现:
int maxProductAfterCutting_Solution2(int length)
{
if(length<2)
return 0;
if(length==2)
return 1;
if(length==3)
return 2;
//尽可能的减去长度为3的绳子段
int timesOf3=length/3;
//当绳子最后剩下的长度为4的时候,不能再减去长度为3的绳子段
//此时更好的方法是把绳子剪成长度为2的两段,因为2*2>3*1
if(length-timesOf3*3==1)
timesOf3-=1;
//最后小于等于4米的,尽量多的产生2米的分割
int timesOf2=(length-timesOf3*3)/2;
//3的多少个三次幂乘以2的多少个2次幂
return (int)(pow(3.0,timesOf3))*(int)(pow(2.0,timesOf2));
}
四、测试及结果
4.1 测试代码
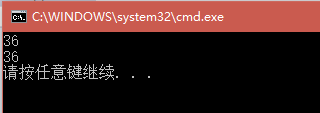
int main()
{
printf("%d\n",maxProductAfterCutting_Solution(10));
printf("%d\n",maxProductAfterCutting_Solution2(10));
return 0;
}